Introduction to Artificial Neural Network Part 1.

Written by Alex Choi, Nov. 09, 2018.

이번 포스팅에서는 인공신경망(Artificial Neural Networks, ANN)에 대하여 간략한 이론을 알아보도록 하겠습니다.

인공신경망(Artificial Neural Networks) 개요

인공신경망은 생물의 뇌가 입력된 자극에 반응하는가를 이해하여 입력 신호와 출력 신호에 대한 관계를 모델링하는 것입니다. 뉴런은 전기 신호를 수집, 처리 및 전파를 주된 목적으로 하는 뇌의 세포인데, 인공신경망에 있어 정보를 처리하는 기본적인 단위를 인공 뉴런(Artificial Neuron) 또는 노드(Node)라고 합니다. 인공신경망은 이러한 거대 병렬 처리를 위한 인공 뉴런들이 서로 연결된 네트워크를 이용하는 것이며, 뇌의 정보 처리 능력이 이러한 뉴런의 네트워크로부터 기인한다고 생각되어, 초창기 인공지능 분야는 인공신경망을 생성하는 것을 목적으로 하였습니다.

인공신경망 분야의 다른 이름은 결합설(Connectionism), 병렬 분산 처리(Parallel Distributed Processing), 신경 계산(Neural Computation) 등이 있습니다.

그렇다면 생물은 몇 개의 뉴런을 가지고 있을까요?

인간은 860억개의 뉴런을 가지고 있으며, 히말라야 원숭이는 63억개, 까마귀는 21억개, 쥐는 7100만개, 바퀴벌레는 100만개, 해파리는 5,600개 정도의 뉴런을 가지고 있습니다. 그런데 가장 많은 뉴런을 가지고 있는 생물은 인간이 아니라 아프리카 코끼리인데 무려 2500억개나 됩니다.

개체	뉴런 수
아프리카 코끼리	257,000,000,000
인간	86,000,000,000
히말라야 원숭이	6,376,000,000
까마귀	2,171,000,000
고양이	760,000,000
문어	500,000,000
기니 피그	240,000,000
골든 햄스터	90,000,000
개구리	16,000,000
바퀴벌레	1,000,000
개미	250,000
과일 파리	250,000
해파리	5,600

출저: wkipedia.org

인류에게 불행인지 다행인지는 몰라도 현재의 인공신경망은 고작 수백개의 뉴런을 가지고 있기 때문에 가까운 미래에 기계가 인류를 위협할 가능성은 없어 보입니다. 그렇지만, 다양한 연구가 빠르게 진행되어 가고 있기 때문에 인공지능의 발전 속도는 점점 가속화 되어 가고 있으며, Neurorobotics 분야에서는 인간이 만든 컴퓨터 알고리즘이 아닌 쥐의 뇌를 이용하여 순수 뉴런을 연결한 네트워크를 통해 모터를 제어하는 단계에까지 이르렀습니다. 다음 영상을 감상해 보겠습니다(소름주의).

ANN 초기 50년간에는 AND, OR, NOT 등 간단한 논리를 처리하는 수준으로 뇌의 동작을 시뮬레이션하는 수준이었으나, 과학자들이 생물학적 뇌의 작동원리를 이해하는데 있어 많은 도움을 주었습니다. 최근 컴퓨팅 파워가 폭발적으로 발전함에 따라 ANN은 실제적인 문제를 푸는데 보다 적극적으로 활용되고 있습니다. 예를 들어, 사물인식, 음성인식, 자율주행차, 날씨예측과 같은 자연현상의 예측과 사회현상의 예측에도 활용되고 있습니다.

즉, ANN은 분류(Classification), 수치 예측, 자율 패턴 인식(Unsupervised Pattern Recognition) 등에 활용할 수 있을 정도로 다재다능합니다. ANN은 입력 데이터와 출력 데이터가 잘 정의되어 있는 문제에 가장 적합한데, 입력 데이터와 출력 데이터 간의 관계를 정의하는 것은 너무나도 복잡합니다.

인공신경망 모델

인공신경망은 인간의 두뇌를 모사한 것이므로 인경신경망의 동작 원리를 이해하려면 뉴런(Neuron)의 동작 원리를 이해하는 것이 중요합니다. 생화학 프로세스를 통해 세포의 수상돌기(Dendrite)로 입력신호가 들어오면, 그 처리의 중요도에 따라 임펄스에 가중치를 부여합니다. 세포체는 입력신호를 누적하고 누적된 입력신호가 일정 임계치를 넘어서면 전기화학 프로세스를 통해 출력신호는 축색돌기(Axon)로 전달됩니다. 축색돌기 종단(Axon Terminal)에서 전기신호는 화학신호로 처리되어 뉴런 간의 작은 간극인 시냅스(Synapse)를 통해 이웃의 뉴런으로 전달됩니다.

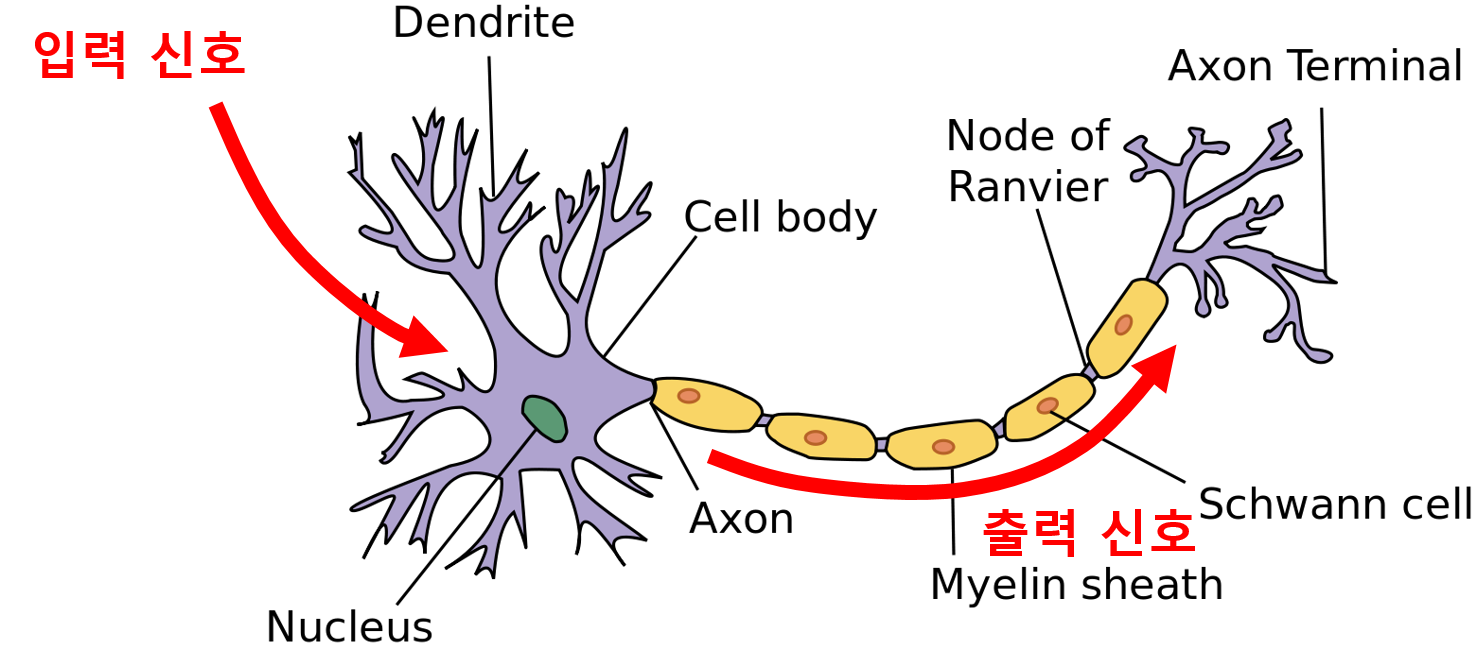
단일 인공 뉴런 모델은 생물학적 모델과 유사하게 이해할 수 있습니다. 아래 그림에서, 노드 \(j\)에서 \(i\)로의 링크는 \(j\)에서 \(i\)로의 활성 \(a_j\) 를 전파하는 역할을 합니다. 각 링크는 이 링크와 관련된 가중치 \(w_{j,i}\) 를 갖는데, 연결성의 강도(Strength) 및 부호(Sign)를 결정합니다.

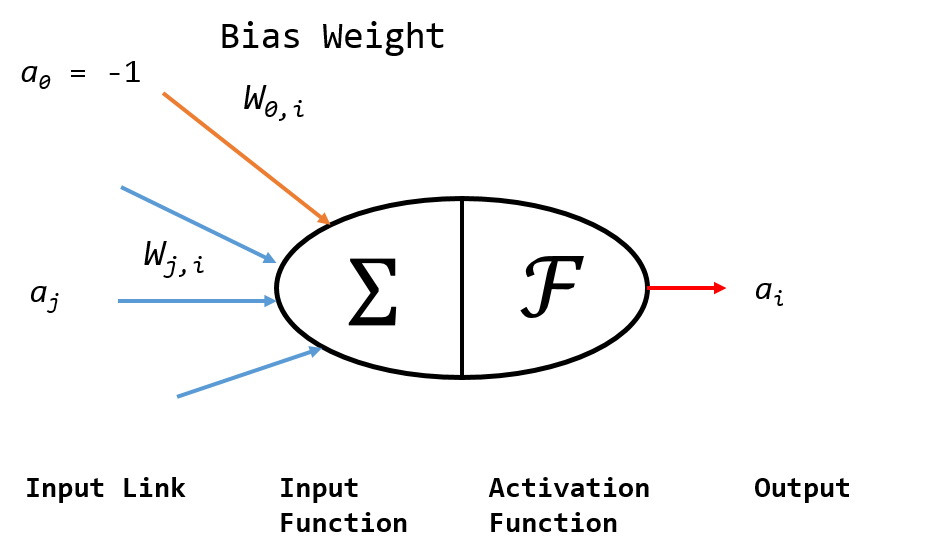
각 노드 \(i\) 는 먼저 입력신호의 가중치합(Weighted Sum)을 계산합니다:

\[\mathbf{Input} = \sum_{j}^{n} w_{j,i}a_{j}\]

이제 출력을 얻으려면 활성 함수(Activation Function) \(\mathscr{F}\) 를 적용합니다:

\[a_{i}=\mathscr{F}(\mathbf{Input}_{i})=\mathscr{F}\begin{pmatrix}\sum_{j=1}^{n}{W_{j,i}a_{j}}\end{pmatrix}\]

특히 \(w_{0,i}\) 를 고정 입력 \(a_{0} = -1\) 에 연결된 편향 가중치라고 합니다. 이런 방식으로 인공신경망은 복잡한 모델을 세우기 위한 구성요소로 뉴런을 사용합니다. 수많은 인공신경망 알고리즘이 존재하지만, 이들은 공동적으로 다음과 같은 특징을 가지고 있습니다:

활성 함수(Activation Function): 뉴런에 연결된 입력신호들을 단일 출력신호로 변환하여 이웃 뉴런으로 전파합니다.
네트워크 토폴로지(Network Topology): 모델의 뉴런과 계층(Layer)이 연결되어 있는 구조입니다.
학습 알고리즘(Training Algorithm): 입력신호에 대응하여 뉴런을 억제하거나 여기시키기 위한 연결 가중치를 결정합니다.

활성 함수(Activation Function)

활성 함수는 인공 뉴런이 유입되는 정보를 처리하고 구성된 네트워크로 전달하는 메커니즘입니다. 인공신경망이 생물학적 신경망을 모사하듯 활성함수 또한 생물학적인 특징을 반영하는 모델을 채용합니다. 생물학적인 측면으로 볼 때, 활성함수는 입력신호를 가중치합을 계산하여 이 값이 정해진 임계치를 넘는지 결정합니다. 만약 임계치를 넘지 못할 경우 아무 일도 하지 않는데, 이를 임계 활성 함수(Threshold Activation Function) (아래 그림 (a))이라고 합니다.

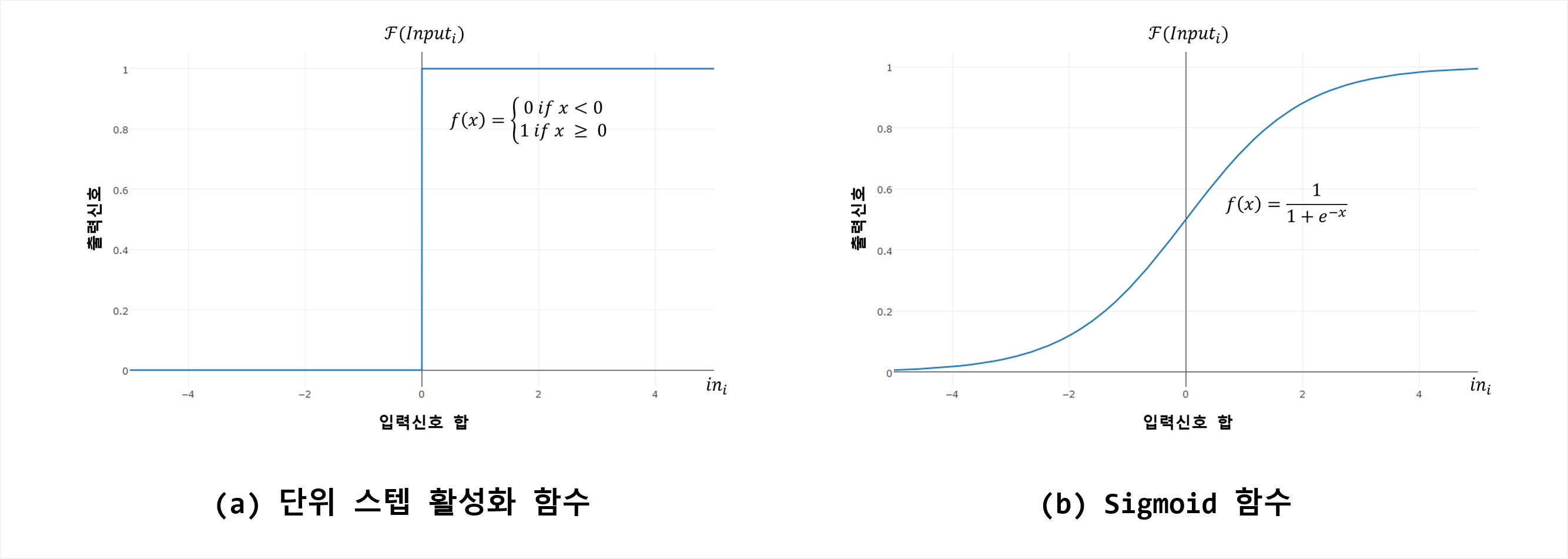
단위 스텝 활성 함수(또는 임계 활성 함수)는 생물학의 동작원리에 부합되기는 하지만 수학적 특성이 바람직하지 않기 때문에 인공신경망에서 거의 사용되지 않습니다. 가장 널리 사용되는 함수는 Sigmoid 활성 함수(또는 Logistic Sigmoid라고도 함)(위의 그림 (b))입니다(사실, Sigmoid 함수도 Saturation 및 Non-zero Centered 특성으로 인해 실무에서 사용하는 것은 바람직하지 않으며, 최근 Rectifier Linear Unit;ReLU이 실무에서 가장 널리 사용됩니다). 출력신호의 범위는 모두 [0, +1]이지만 Sigmoid 함수는 입력신호 범위 전체에서 미분가능합니다. Sigmoid 활성함수의 미분가능 특성 덕분에 ANN 최적화 알고리즘을 적용할 수 있습니다.

네트워크 토폴로지(Network Topology)

토폴로지(Topology)는 우리말로 위상기하학이라고 하며, 오브젝트의 연결성(Connectivity)와 관련이 있습니다. ANN에서의 토폴로지는 뉴런 간의 연결구조(또는 패턴)를 의미하며, 이 연결구조가 ANN의 학습능력을 결정합니다. 토폴로지는 다음과 같이 분류할 수 있습니다:

레이어의 개수
네트워크 내의 정보의 역방향 이동 가능성
네트워크의 각 레이어의 노드 개수

토폴로지는 네트워크를 통해 학습 가능한 태스크의 복잡성을 결정하며, 일반적으로 네트워크가 복잡해지고 규모가 커질수록 다양한 패턴과 복잡한 결정 경계를 식별할 수 있습니다. 네트워크의 성능은 그 크기뿐만 아니라 노드들이 어떻게 배치되어 있는가에 의해서도 결정됩니다.

레이어(Layer)의 개수

ANN의 처리 능력은 곧 레이어의 개수와 밀접한 관계가 있습니다. 레이어는 입력노드와 출력노드의 집합체이며, 입력노드는 입력 데이터로부터 신호를 받는 뉴런을 일컫습니다. 각 입력노드는 활성함수를 통해 입력신호를 변환하며 이를 출력노드로 전달한다. 아래 그림은 2개의 입력데이터와 2개의 입력 노드로 구성된 1개의 은닉 레이어(Hidden Layer)로 구성된 간단한 ANN 모델이며, 레이어가 1개 존재하므로 단일 레이어 네트워크(Single-Layer Network)라고 합니다. 이 모델은 너무 단순하므로 선형으로 분류가능한(Linearly Separable) 패턴에 대한 문제에만 적용이 가능하며, 보다 정교한 문제를 풀기 위해서는 좀 더 복잡한 모델이 요구됩니다.

아래 그림과 같이 1개 이상의 은닉 레이어가 추가된 네트워크를 다중 레이어 네트워크(Multi-Layer Network)라고 하며, 입력노드들에서 출력노드 사이에 은닉 노드들이 존재합니다.

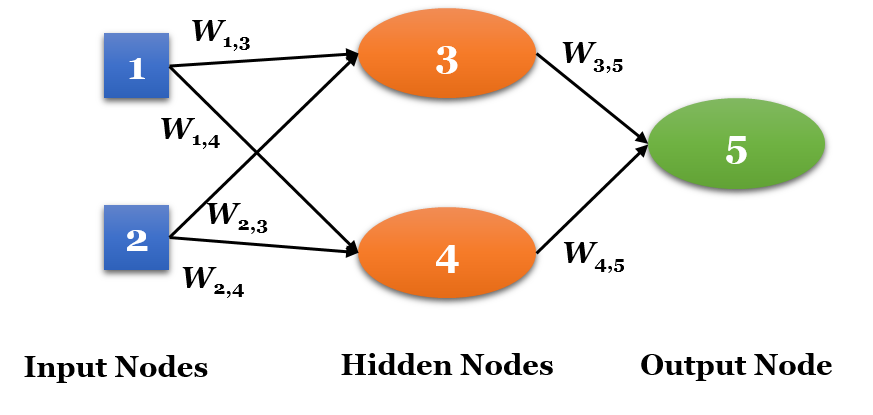
정보의 이동 방향

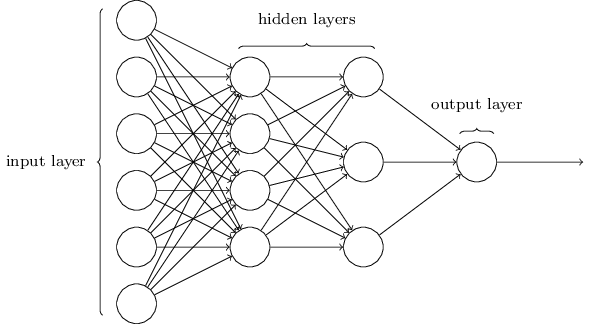
앞서 언급한 네트워크에서 정보는 항상 입력노드에서 시작하여 출력노드로 종결되는 구조였습니다. 이처럼 정보가 한 방향으로만 진행되는 네트워크를 피드포워드 네트워크(Feedforward Network)라고 하며, 특히 아래의 그림과 같이 다중의 은닉 레이어, 즉 2개 이상의 은닉 레이어를 갖는 네트워크 구조를 딥 뉴럴 네트워크(Deep Neural Network; DNN)라고 하며, 이를 이용한 Learning(Training)을 딥 러닝(Deep Learning)이라고 합니다.

딥 러닝은 바둑에서 이세돌을 4:1로 누른 DeepMind(Google의 자회사)의 알파고(AlphaGo)의 근간이 되는 알고리즘입니다. 다중 레이어 피드포워드 네트워크는 다중 레이어 퍼셉트론(Multi-Layer Perceptron; MLP)라고도 불리우며 사실상 ANN 토폴로지의 표준이라고 할 수 있습니다.

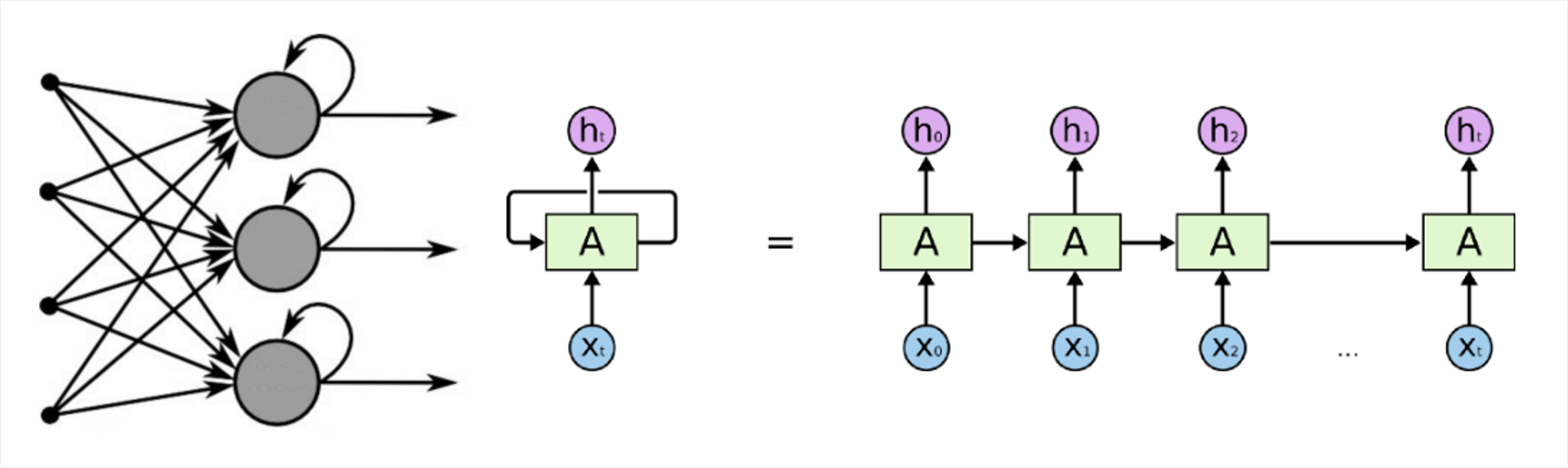
이미지 출처: http://neuralnetworksanddeeplearning.com/chap1.html

피드포워드 네트워크와는 달리 루프(Loop)에 의해서 정보가 양방향으로 이동하는 네트워크를 반복 네트워크(Recurrent Network) 또는 피드백 네트워크(Feedback Network)라고 합니다. 피드백 네트워크는 좀 더 생물학적인 뉴럴 네트워크를 모사하며 매우 복잡한 패턴을 학습하는데 사용됩니다. 예를 들어 지연(Delay)을 추가하여 주식시장의 예측, 날씨 예측 등 단기 기억을 통해 네트워크의 성능을 높일 수 있으므로, 일정 기간의 일련의 이벤트들을 이해할 수 있는 능력을 지니고 있습니다. 그러나, 너무 복잡하여 현재로서는 이론상에 머무는 수준이며 실제 문제에 거의 적용되지 못하고 있는 실정입니다 (그럼에도 이 방법은 가장 유망한 방법 중 하나인데, 자연어처리(Natural Language Processing;NLP), 로봇제어, 인공지능 기반 작곡 등 Sequence Data를 처리하는데 유용하기 때문입니다).

각 레이어 내 노드 개수

네트워크 토폴로지를 결정하는 또다른 요인은 각 레이어 내에 존재하는 노드의 개수입니다. 당연히 각 레이어에 대한 노드의 개수가 증가할 수록 네트워크 토폴로지의 복잡도는 증가합니다. 입력노드의 개수는 입력 데이터의 Feature의 수에 의해 미리 결정되며, 출력노드의 개수 또한 모델의 결과에 따라 또는 모델의 분류 수준에 따라 결정되지만, 은닉 노드들의 수는 사용자가 자유롭게 결정할 수 있습니다. 은닉 레이어의 뉴런 개수를 결정하는 신뢰할만한 어떤 법칙이 존재하는 것은 아니지만, 적정한 뉴런의 개수는 입력 노드, 학습 데이터 량, 노이즈 데이터 량, 학습 작업의 복잡도 등과 관련이 있습니다. 일반적으로 네트워크 토폴로지가 복잡할수록 더 복잡한 문제에 대한 학습을 할 수 있습니다. 그러나 노드의 개수가 적정수보다 과도하게 많을 경우 Overfitting의 위험이 있으며, 계산량 또한 많아지므로 학습속도가 느려집니다. 최선의 적용은 적절한 성능을 내는 최소의 노드개수를 사용하는 것입니다. 대부분의 경우 적은 개수의 은닉 노드만으로도 엄청난 양의 학습 능력을 제공할 수 있습니다.

역전파

네트워크 토폴로지 그 자체는 갓 태어난 아기처럼 아무 것도 배우지 않은 비어있는 석판과도 같습니다. 입력되는 데이터를 처리하는 과정을 통해 뉴런 간 연결성이 강화되거나 약화되며, 그 과정을 통해 패턴을 인식하는 수준으로 네트워크 연결에 대한 가중치가 형성되어 갑니다. 이론상으로는 수십년전에 정립되었음에도 불구하고, 연결 가중치를 조절하는 신경망 학습은 막대한 컴퓨터 연산량으로 인해 효율적인 알고리즘이 발견된 1980년대 후반이 되어서야 겨우 실질적인 (간단한) 문제를 풀 수 있는 수준이 되었습니다. 그 실효율적인 알고리즘은 현재 역전파(Backpropagation)이라고 알려진 역전파되는 에러 전략(Strategy of Back-propagating Errors)입니다. 다른 기계학습 알고리즘들에 비해 여전히 느리기로 악명이 높지만, 영화 "아바타(Avatar)"가 스테레오스코픽의 부흥을 이끌어냈듯 역전파 방법은 ANN에 다시금 관심을 모으는 원동력이 되었습니다. 그리고 결과적으로 이제는 역전파 알고리즘을 사용하는 다중 레이어 피드포워드(Multi-Layer Feedforward) 네트워크는 데이터 마이닝의 필수가 되었습니다.

역전파 알고리즘의 강점과 약점을 다음과 같습니다:

강 점	약 점
분류 또는 예측 문제에 적용 가능함.	컴퓨터 연산량이 매우 많고 학습속도가 극히 느림. 특히 네트워크 토폴로지가 복잡한 경우 더욱 심각함.
거의 모든 알고리즘이 할 수 있는 것보다 훨씬 더 복잡한 패턴의 모델링이 가능함.	학습 데이터에 대한 과적응(Ovefitting) 경향이 강함.
되도록 데이터의 근원적인 관계에 대한 가정을 적게 함.	해석이 거의 불가능하며 가능하다고 해도 매우 어렵고 복잡한 블랙박스 모델임.

역전파 알고리즘의 일반적인 형태는 많은 반복 사이클을 갖는 두 개의 프로세스를 포함하며, 각 사이클을 Epoch라고 합니다. 네트워크는 어떠한 사전 지식도 갖고 있지 않으므로, 초기 가중치는 랜덤으로 설정되며, 정해진 중단 조건을 만족할 때까지 프로세스를 통해 반복됩니다.

각각의 Epoch는 다음과 같은 Phase를 포함합니다:

(1) 순방향 Phase: 뉴런이 입력 레이어에서 출력 레이어 순으로 활성되며 그에 따라 뉴런의 가중치와 활성 함수을 적용합니다. 마지막 레이어에 도달하면 출력신호가 생성됩니다.

(2) 역방향 Phase: 순방향 Phase에서 얻은 네트워크 출력신호와 학습 데이터의 실제 타겟값과 비교합니다. 그 두 개의 값 사이의 차이가 에러를 일으키면 네트워크에서 역방향으로 전파시켜 뉴런들 간의 연결 가중치를 수정하여 향후 에러를 지속적으로 줄여나갑니다.

이런 식으로 네트워크는 역방향으로 보낸 정보를 이용하여 네트워크의 전체 에러를 줄여나갑니다. 그렇다면 이때쯤 하나의 의문사항이 듭니다: 과연 뉴런의 입력과 출력 사이의 관계가 그렇게 복잡한대 도대체 어떻게 이 알고리즘은 가중치의 변화량을 결정하는 것일까? 이에 대한 해답은 급경사법(Steepest Descent Method)에 있습니다. 급경사법은 간단히 산 위에서 눈을 가린 채로 가장 낮은 곳을 찾아갈 때 쓰는 방법과도 같습니다. 사방을 지팡이로 두드려보고 가장 경사가 아래 방향으로 심한 곳으로 현재 위치한 지점에서 한 발자국가고 그 위치에서 다시 가장 경사가 아래로 심한 방향을 찾고 그 방향으로 한 발자국씩 이동합니다. 따라서, 급경사법은 방향탐색(Direction Search)과 스텝크기 결정(Step Size Determination)으로 구성됩니다.

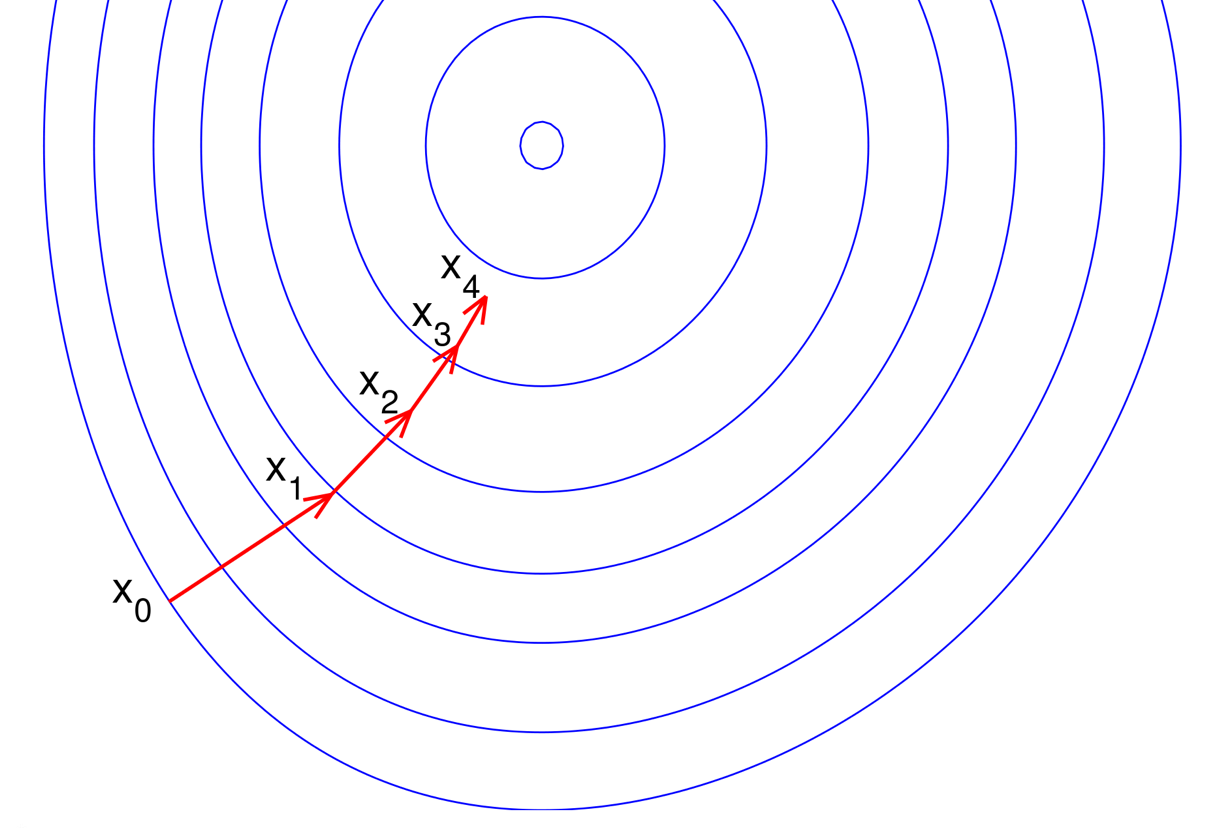
이미지 출처: http://aria42.com/blog/2014/12/understanding-lbfgs

위의 이미지를 살펴보도록 합니다. 산의 높이를 등고선으로 표현하였을 때 각 등고선에 수직한 방향(빨간 화살표)이 급강하방향입니다 (내부 동심원이 가장 낮은 등고선이라 가정). 참고로, 내부 동심원이 가장 등고선 높이가 크다고 가정하면 빨간 화살표는 급상승(Steepest Ascent)방향이 되며, 급강하와 급상승은 단지 부호가 바뀐다는 것뿐입니다.

상기 이미지의 파란 등고선에 표면함수(Surface Function)이 \(z = f(x,y)\)로 주어졌다면 특정 위치 \((x*, y*)\) 에서의 급강하방향은 다음의 벡터(Vector)로 표현됩니다:

\(-\nabla f(x^{*},y^{*})=-\begin{bmatrix}\partial f(x^{*},y^{*})/\partial x \\ \partial f(x^{*},y^{*})/\partial y\end{bmatrix}\)

이와 유사하게 역전파 알고리즘은 각 뉴런의 활성함수의 미분값을 이용하여 각각의 유입 가중치의 방향으로 경사도를 파악합니다. 이 때문에 활성함수의 미분가능성이 중요한 의미를 지닙니다. 이 경사도는 가중치의 변화에 대하여 에러의 증감이 얼마나 급속하게 변화되는지를 판단할 수 있는 기준을 제시합니다. 알고리즘은 학습률(Learning Rate)라고 하는 양에 의해 에러가 급속도로 작아지는 방향으로 가중치를 변화시킵니다. 학습률이 커질 수록 초기에는 빠르게 에러를 줄이나 해(Solution) 근처에서는 오버슈팅(Overshooting)으로 인해 수렴 속도가 느려지거나 재수가 없는 경우 영원히 수렴하지 못하는 경우가 있습니다. 또한, 급강하법은 지역최소값(Local Minimum)은 찾을 수 있으나 전역최소값(Global Minimum)을 찾지 못하는 단점이 있습니다.

이제 이론적인 것을 다룬 Part 1.을 마무리하고 Part 2.에서는 R의 인공신경망 패키지인 nerualnet을 이용하여 ANN 알고리즘으로 실질적인 예제를 풀어보도록 하겠습니다.