Deep Learning from Scratch Part 1.
Written by Alex Choi, Feb. 21, 2017.
이 글은 Parallel R의 R for Deep Learning (I): Build Fully Connected Neural Network from Scratch를 번역한 것입니다.
- Source Code: DNN from Scratch.zip
- GitHub: https://github.com/PatricZhao/ParallelR
이론적 배경
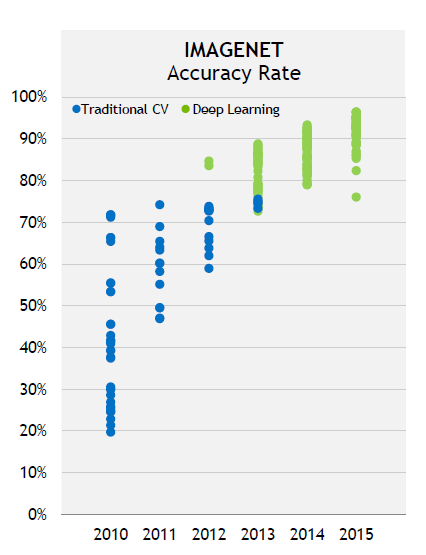
심층 인공신경망(이하 원어 사용: Deep Neural Network; DNN)는 최근 몇년간 이미지 인식, 자연어 처리 및 자율주행차 분야에서 막대한 성과를 이루어 냈으며, 그림 1.에서 보이는 바와 같이 2012년에서 2015년 사이 DNN은 IMAGNET의 정확도를 80%에서 95%까지 끌어올렸습니다. 이는 전통적인 컴퓨터 비전(Computer Vision; CV) 방법론들을 꺾은 것입니다.
이 글에서는 데이터 과학 분야에서 공통적으로 DNN이라 부르는 Fully Connected Neural Networks에 대해 집중적으로 다루고자 합니다. DNN의 가장 큰 장점은, Kaggle의 예제처럼 엔지니어가 쉽게 정의할 수 없는 복잡하고 고차원적인 데이터를 Deep Layers 아키텍쳐를 이용하여 자동으로 피쳐(Feature)들을 추출하고 학습할 수 있다는 것입니다. 따라서, DNN은 데이터 과학자들에게 매우 매력적이며, Nick이 쓴 글과 DNN을 이용한 신용점수 매기기처럼 분류(Classification), 시계열(Time Series), 추천 등의 분야에서 성공적인 케이스가 존재합니다. CRAN과 R 커뮤니티에 nnet, nerualnet, H2O, DARCH, deepnet 및 mxnet 등과 같은 인기가 많고 성숙한 DNN 패키지들이 많이 존재하지만, H2O DNN 알고리즘-R 인터페이스를 강력하게 권장합니다.
| 패키지 | 백엔드 | 컴퓨터 자원 |
|---|---|---|
| nnet | C/C++ | 싱글 스레드 (Single Thread) |
| neuralnet | C/C++ | 싱글 스레드 (Single Thread) |
| DARCH | C/C++ | 싱글 스레드 (Single Thread) |
| deepnet | R | 싱글 스레드 (Single Thread) |
| h2o | Java | 멀티-스레드, 멀티-노드 |
| mxnet | C/C++/CUDA | 멀티-스레드, GPU, 멀티-노드 |
그러면 굳이 DNN을 바닥부터 구현할 필요가 있는 것일까요?
– 신경망의 작동 원리를 이해할 수 있습니다
대부분의 경우 기존의 DNN 패키지를 이용하여 DNN 모델에 대한 한 줄의 R 코드만으로 해결할 수 있는데, neuralnet 패키지의 예가 그렇습니다. 그러나, 경험이 없는 유저라면 처리 과정과 결과를 이해하기 어려울 수 있습니다. 따라서, 메커니즘에서 연산 시각에 이르는 보다 상세한 내용을 이해하려면 자신만의 네트워크를 구현해 보는 연습이 매우 가치있는 작업일 것입니다.
– 자신의 새로운 아이디어를 네트워크에 접목할 수 있다
DNN은 급속도로 발전하는 분야 중 하나입니다. 많은 훌륭한 작업과 연구 결과들이 톱저널과 인터넷에 매주마다 게재되며, 유저들은 자신들의 특정 네트워크 설정이 다양한 활성 함수(Activation Function), 손실 함수(Loss Function), 정규화(Regularization), 연결 그래프 등의 문제를 만족하도록 하고 있다. 반면에 기존의 패키지들은 분명 최근의 연구를 모두 반영하지는 못하고 있으며, 기존의 거의 대부분의 패키지들은 C/C++, Java로 작성되었기 때문에 최근의 변화와 당신의 아이디어에 유연하게 대응하지 못합니다.
– 네트워크와 데이터를 디버깅하고 시각화할 수 있다
언급한 바와 같이, 기존의 DNN 패키지들은 고도로 조합되었으며 저수준 언어로 작성되었기 때문에 레이어 별로 또는 노드 별로 네트워크를 디버깅하는 것은 악몽과도 같은 것입니다. 각 레이어의 결과를 시각화하는 것이 쉬운 일은 아니더라도, 학습 과정 동안 데이터 또는 Weight들을 모니터링하고 네트워크에서 발견된 패턴들을 시각화하는 것은 중요합니다.
기본 개념과 구성요소
데이터 과학에서 DNN이라고 부르는, Fully Connected Neural Network는 인접하는 네트워크 레이어 간에 완전히 연결되는 네트워크이다. 네트워크 내 모든 뉴런이 인접하는 레이어의 모든 뉴런과 연결되는 것입니다.
아래의 그림은 1개의 입력 레이어, 2개의 은닉 레이어, 1개의 출력 레이어로 구성된 매우 간단하고 전형적인 네트워크를 보여줍니다. 대부분 연구자들이 네트워크 아키텍쳐에 대해 언급할 때, 이는 네트워크 내의 레이어 개수, 각 레이어 내 뉴런의 개수, 사용된 활성함수, 손실함수, 정규화의 형태 등과 같은 DNN의 설정을 일컫습니다.
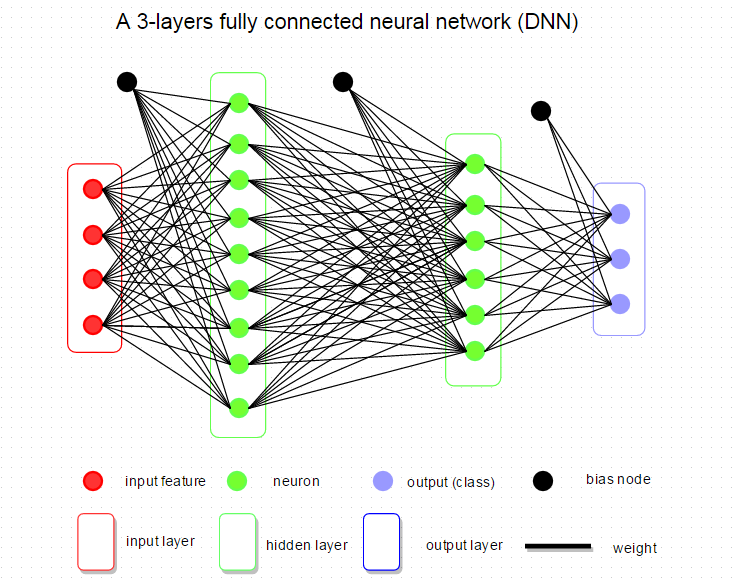
이제 DNN의 기본 구성요소를 훑어보고 이것이 R에서 어떻게 구현되는지 알아보도록 하겠습니다.
Weight와 Bias
위의 DNN 아키텍쳐를 예를 들어보면, 3개의 Weight 그룹이 있는데, 입력 레이어에서 첫번째 은닉 레이어까지, 첫번째 은닉 레이어에서 두번째 은닉 레이어까지, 두번째 은닉 레이어에서 출력 레이어까지입니다. Bias 단위는 모든 은닉 노드로 연결되며 이는 출력 점수에 영향을 주지만 실제 데이터와 상호작용이 없는 것을 가정합니다.
R에서의 구현에서 Weight와 Bias는 행렬로 표현합니다. Weight의 크기는 다음과 같이 정의합니다:
(레이어 M 내 뉴런의 개수) X (레이어 M+1 내 뉴런의 개수)
그리고 Weight들은 rnorm으로부터 임의로 초기화 됩니다. Bias는 단지 뉴런의 크기와 동일한 1차원 행렬이며 0으로 설정됩니다. 1/sqrt(n)을 이용한 분산 보정과 Sparse 초기화와 같은 다른 초기화 방법은 Stanford CS231n의 Weight Initialization에 소개되어 있습니다.
R CODE:
weight.i <- 0.01*matrix(rnorm(layer.size(i)*layer.size(i+1)),
nrow=layer.size(i),
ncol=layer.size(i+1))
bias.i <- matrix(0, nrow=1, ncol = layer.size(i))
다른 일반적인 구현 방법은 Weight들과 Bias를 결합하여 입력 차원이 N+1이 되도록 하는 것인데, N은 아래와 같이 1개의 Bias를 갖는 입력 피쳐의 개수입니다.
weight <- 0.01*matrix(rnorm((layer.size(i)+1)*layer.size(i+1)),
nrow=layer.size(i)+1,
ncol=layer.size(i+1))
뉴런(Neuron)
뉴런은 인간의 생물학적 뉴런 모델에서 영감을 얻은 DNN의 기본 단위입니다. 하나의 뉴런은 데이터 과학의 선형 회귀분석과 같이 Weight과 입력을 곱하고 더하는 연산을 수행(FMA)하는데, FMA의 결과는 활성함수로 전달됩니다. 주로 사용되는 활성함수들에는 sigmoid, ReLu, Tanh 및 Maxout 등이 있습니다. 이 글에서는 Rectified Linear Unit (ReLU), f(x) = max(0, x)를 활성함수로 사용할 것입니다. 다른 활성함수에 대해 알아보려면 여기를 참고하도록 합니다.
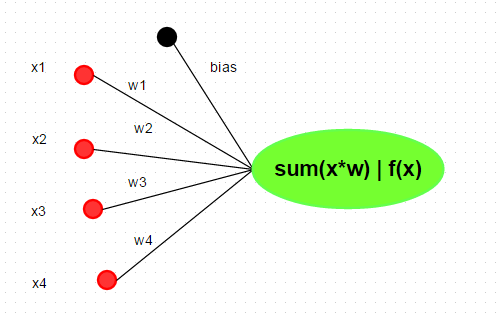
R에서 sum(xi*wi)과 같이 다양한 방법으로 뉴런을 구현할 수 있지만, 보다 효율적인 표현은 행렬 곱셈을 이용하는 것입니다.
neuron.ij <- max(0, input %*% weight + bias)
구현 팁
실질적으로, 성능을 고려하여 항상 일괄적으로 레이어 내 모든 뉴런을 업데이트합니다. 따라서, 위의 코드는 제대로 동작하지 않을 것입니다.
1) 행렬 곱셈과 덧셈
아래의 코드에서 보는 바와 같이, 서로 다른 차원을 갖는 input %*% weights와 bias를 직접 더할 수는 없습니다. 이에 대한 두가지 솔루션이 있습니다. 첫번째는 Bias를 ncol번 반복하는 것인데, 크기가 큰 데이터 입력에 대하여 메모리를 낭비할 수 있기 때문에 두번째 방법이 더 낫습니다.
# dimension: 2X2
input <- matrix(1:4, nrow=2, ncol=2)
# dimension: 2x3
weights <- matrix(1:6, nrow=2, ncol=3)
# dimension: 1*3
bias <- matrix(1:3, nrow=1, ncol=3)
# doesn't work since unmatched dimension
input %*% weights + bias
Error input %*% weights + bias : non-conformable arrays
# solution 1: repeat bias aligned to 2X3
s1 <- input %*% weights + matrix(rep(bias, each=2), ncol=3)
# solution 2: sweep addition
s2 <- sweep(input %*% weights ,2, bias, '+')
all.equal(s1, s2)
[1] TRUE
2) 행렬에 대한 요소 최대값
여기에서 다른 트릭은 pmax를 max로 교체하여 행렬 전체의 최대값 대신 행렬의 요소에 대한 최대값을 얻는 것인데, 특히 pmax의 순서에 유의해야 합니다.
# the original matrix
> s1
[,1] [,2] [,3]
[1,] 8 17 26
[2,] 11 24 37
# max returns global maximum
> max(0, s1)
[1] 37
# s1 is aligned with a scalar, so the matrix structure is lost
> pmax(0, s1)
[1] 8 11 17 24 26 37
# correct
# put matrix in the first, the scalar will be recycled to match matrix structure
> pmax(s1, 0)
[,1] [,2] [,3]
[1,] 8 17 26
[2,] 11 24 37
레이어(Layer)
입력 레이어
입력 레이어는 1개의 레이어로 상대적으로 고정되어 있으며 기본 개수는 입력 데이터의 피쳐(Feature) 개수와 동일합니다.
은닉 레이어
은닉 레이어는 매우 다양하며 DNN의 핵심 구성요소입니다. 그러나 일반적으로 문제가 복잡할수록(비선형) 바람직한 패턴을 찾기 위해서는 더 많은 은닉 레이어가 필요합니다.
출력 레이어
출력 레이어의 단위는 Classification에 있어서는 각 클래스의 점수를 표현하기 위해 사용되고 회귀분석에 있어서는 임의의 실수 값을 나타내기 때문에 일반적으로 활성함수를 갖지 않습니다. 회귀분석에 대해서 출력 노드는 단 한 개이지만, Classification에 있어서는 출력 단위의 개수는 예측의 카테고리의 개수와 일치합니다.
신경망 구축하기: 아키텍쳐, 예측 그리고 학습
지금까지, Deep Neural Network의 기본 개념에 대해 알아보았으며, 이제 Deep Neural Network을 구축해 보려고 하는데, 이는 네트워크 아키텍쳐, 학습 네트워크를 결정하는 것과 학습된 네트워크를 가지고 새로운 데이터를 예측하는 일을 포함합니다. 쉽게 이해하기 위해서, 우리는 작은 데이터세트인 Edgar Anderson의 데이터(iris)를 사용하여 DNN으로 Classification을 수행하고자 합니다.
네트워크 아키텍쳐
IRIS는 잘 알려진 머신러닝용 stock R의 빌트인(Built-In) 데이터세트입니다. 따라서 아래와 같이 콘솔에서 직접 summary를 통해 데이터세트를 확인할 수 있습니다.
summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Summary로부터 4개의 피쳐와 3개의 Species 카테고리가 있음을 알 수 있습니다. 그래서 아래와 같이 DNN 아키텍쳐를 설계할 수 있습니다.
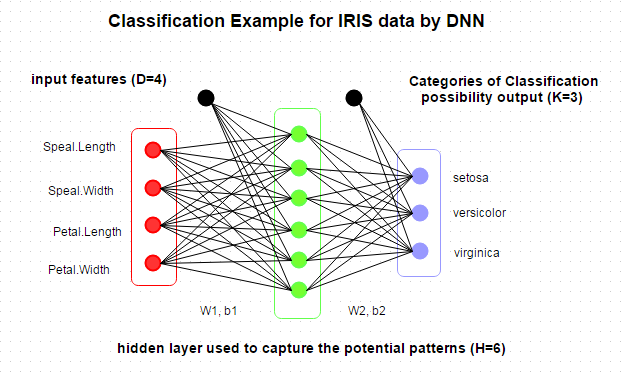
그리고나서 list로 DNN 모델을 저장할 수 있는데, 이것은 아래와 같이 저장 또는 예측을 위해 사용될 수 있습니다. 사실, 유연하게 모델에 대한 더많은 관심 파라미터들을 저장할 수 있습니다.
List of 7
$ D : int 4
$ H : num 6
$ K : int 3
$ W1: num [1:4, 1:6] 1.34994 1.11369 -0.57346 -1.12123 -0.00107 ...
$ b1: num [1, 1:6] 1.336621 -0.509689 -0.000277 -0.473194 0 ...
$ W2: num [1:6, 1:3] 1.31464 -0.92211 -0.00574 -0.82909 0.00312 ...
$ b2: num [1, 1:3] 0.581 0.506 -1.088
예측
머신러닝 분야에서 Classification 또는 추론이라고도 불리우는 예측은 학습와 비교할 때 함축적인 개념이며 행렬 곱셈을 통해 입력으로부터 출력 레이어 간 네트워크를 훑고 지나갑니다. 출력 레이어는 활성함수를 필요로 하지 않습니다. 회귀분석에서는 출력은 예측된 실수 값을 나타내는 반면, Classification에서는 softmax에 의해 확률이 계산될 것입니다. 이 과정은 Feed Forward 또는 Feed Propagation이라고 불리웁니다.
# Prediction
predict.dnn <- function(model, data = X.test) {
# new data, transfer to matrix
new.data <- data.matrix(data)
# Feed Forwad
hidden.layer <- sweep(new.data %*% model$W1 ,2, model$b1, '+')
# neurons : Rectified Linear
hidden.layer <- pmax(hidden.layer, 0)
score <- sweep(hidden.layer %*% model$W2, 2, model$b2, '+')
# Loss Function: softmax
score.exp <- exp(score)
probs <-sweep(score.exp, 1, rowSums(score.exp), '/')
# select max possiblity
labels.predicted <- max.col(probs)
return(labels.predicted)
}
학습
학습은 주어진 네트워크 아키텍쳐에서 최적화 파라미터(Weight들과 Bias)를 찾고 Classification 오차 또는 잔류오차를 최소화하는 것입니다. 이 과정은 Feed Forward와 Back Propagation의 두 개의 파트로 나눌 수 있습니다. Feed Forward는 입력 데이터 (예측 부분)를 갖는 네트워크를 훑고 지나가고 Loss Function (Cost Function)으로 출력 레이터의 데이터 손실을 계산합니다. "데이터 손실은 예측(가령, Classification에서 Class 점수 실지 검증 라벨) 간의 호환성을 측정합니다." 본 예제 코드에서 데이터 손실을 평가하기 위해 Cross-Entropy 함수를 선택하였으며 이에 대한 자세한 내용은 여기를 참고하기 바랍니다.
데이터 손실값을 얻은 후, Weights와 Bias를 변경하여 데이터 손실을 최소화해야 합니다. 가장 많이 사용되는 방법은 각 파라미터(W1, W2, b1, b2)에 대하여 데이터 손실의 미분을 계산해야 하는 급강하법(Gradient Descent)이나 확률적 급강하법(Stochastic Gradient Descent)으로 모든 레이어와 뉴런으로 손실을 역전파(Back Propagation)시키는 것입니다. 역전파는 다양한 활성함수에 다라 달라질 것이며 역전파식과 방법은 여기와 여기를 참고하기 바랍니다. Stanford CS231n에서 더 자세한 팁을 얻을 수 있습니다.
본 예제에서 ReLU에 대한 각 포인트에 대한 미분은:

# Train: build and train a 2-layers neural network
train.dnn <- function(x, y, traindata=data, testdata=NULL,
# set hidden layers and neurons
# currently, only support 1 hidden layer
hidden=c(6),
# max iteration steps
maxit=2000,
# delta loss
abstol=1e-2,
# learning rate
lr = 1e-2,
# regularization rate
reg = 1e-3,
# show results every 'display' step
display = 100,
random.seed = 1)
{
# to make the case reproducible.
set.seed(random.seed)
# total number of training set
N <- nrow(traindata)
# extract the data and label
# don't need atribute
X <- unname(data.matrix(traindata[,x]))
Y <- traindata[,y]
if(is.factor(Y)) { Y <- as.integer(Y) }
# updated: 10.March.2016: create index for both row and col
Y.len <- length(unique(Y))
Y.set <- sort(unique(Y))
Y.index <- cbind(1:N, match(Y, Y.set))
# number of input features
D <- ncol(X)
# number of categories for classification
K <- length(unique(Y))
H <- hidden
# create and init weights and bias
W1 <- 0.01*matrix(rnorm(D*H), nrow=D, ncol=H)
b1 <- matrix(0, nrow=1, ncol=H)
W2 <- 0.01*matrix(rnorm(H*K), nrow=H, ncol=K)
b2 <- matrix(0, nrow=1, ncol=K)
# use all train data to update weights since it's a small dataset
batchsize <- N
# updated: March 17. 2016
# init loss to a very big value
loss <- 100000
# Training the network
i <- 0
while(i < maxit && loss > abstol ) {
# iteration index
i <- i +1
# forward ....
# 1 indicate row, 2 indicate col
hidden.layer <- sweep(X %*% W1 ,2, b1, '+')
# neurons : ReLU
hidden.layer <- pmax(hidden.layer, 0)
score <- sweep(hidden.layer %*% W2, 2, b2, '+')
# softmax
score.exp <- exp(score)
probs <-sweep(score.exp, 1, rowSums(score.exp), '/')
# compute the loss
corect.logprobs <- -log(probs[Y.index])
data.loss <- sum(corect.logprobs)/batchsize
reg.loss <- 0.5*reg* (sum(W1*W1) + sum(W2*W2))
loss <- data.loss + reg.loss
# display results and update model
if( i %% display == 0) {
if(!is.null(testdata)) {
model <- list( D = D,
H = H,
K = K,
# weights and bias
W1 = W1,
b1 = b1,
W2 = W2,
b2 = b2)
labs <- predict.dnn(model, testdata[,-y])
# updated: 10.March.2016
accuracy <- mean(as.integer(testdata[,y]) == Y.set[labs])
cat(i, loss, accuracy, "\n")
} else {
cat(i, loss, "\n")
}
}
# backward ....
dscores <- probs
dscores[Y.index] <- dscores[Y.index] -1
dscores <- dscores / batchsize
dW2 <- t(hidden.layer) %*% dscores
db2 <- colSums(dscores)
dhidden <- dscores %*% t(W2)
dhidden[hidden.layer <= 0] <- 0
dW1 <- t(X) %*% dhidden
db1 <- colSums(dhidden)
# update ....
dW2 <- dW2 + reg*W2
dW1 <- dW1 + reg*W1
W1 <- W1 - lr * dW1
b1 <- b1 - lr * db1
W2 <- W2 - lr * dW2
b2 <- b2 - lr * db2
}
# final results
# creat list to store learned parameters
# you can add more parameters for debug and visualization
# such as residuals, fitted.values ...
model <- list( D = D,
H = H,
K = K,
# weights and bias
W1= W1,
b1= b1,
W2= W2,
b2= b2)
return(model)
}
테스트 및 시각화
2개의 레이어를 갖는 간단한 DNN 모델을 구성하였으니 이제 우리의 모델을 테스트할 수 있게 되었습니다. 먼저, 데이터세트를 학습용과 테스트용 그룹으로 분리하고 학습 데이터세트를 이용하여 학습 모델을 세우는 한편 테스트 데이터세트를 이용하여 우리의 모델의 일반화 가능성을 측정하고자 합니다.
########################################################################
# testing
#######################################################################
set.seed(1)
# 0. EDA
summary(iris)
plot(iris)
# 1. split data into test/train
samp <- c(sample(1:50,25), sample(51:100,25), sample(101:150,25))
# 2. train model
ir.model <- train.dnn(x=1:4, y=5, traindata=iris[samp,], testdata=iris[-samp,], hidden=6, maxit=2000, display=50)
# 3. prediction
labels.dnn <- predict.dnn(ir.model, iris[-samp, -5])
# 4. verify the results
table(iris[-samp,5], labels.dnn)
# labels.dnn
# 1 2 3
#setosa 25 0 0
#versicolor 0 24 1
#virginica 0 0 25
#accuracy
mean(as.integer(iris[-samp, 5]) == labels.dnn)
# 0.98
학습 데이터세트의 데이터 손실과 정확도는 아래와 같습니다:
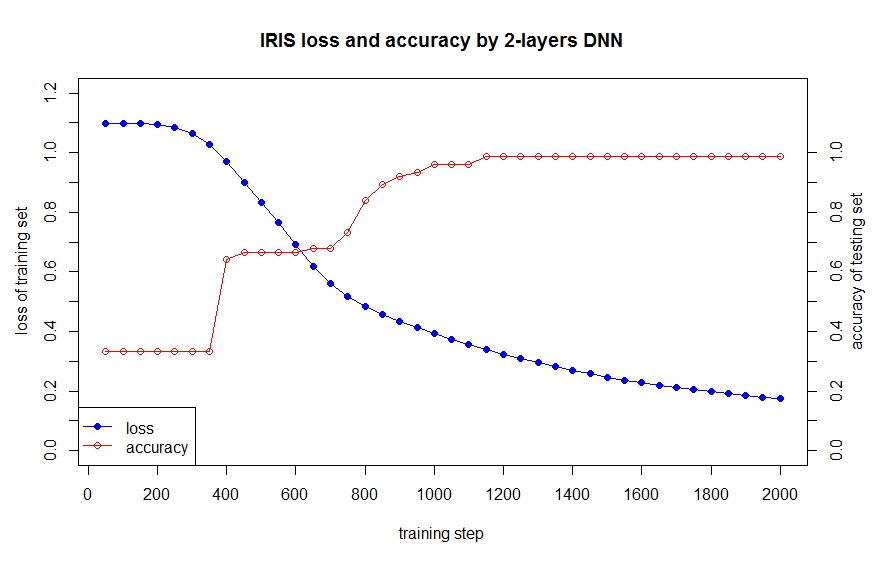
아래의 코드와 같이, 작성한 DNN 모델과 nnet 패키지를 비교하였습니다.
library(nnet)
ird <- data.frame(rbind(iris3[,,1], iris3[,,2], iris3[,,3]),
species = factor(c(rep("s",50), rep("c", 50), rep("v", 50))))
ir.nn2 <- nnet(species ~ ., data = ird, subset = samp, size = 6, rang = 0.1,
decay = 1e-2, maxit = 2000)
labels.nnet <- predict(ir.nn2, ird[-samp,], type="class")
table(ird$species[-samp], labels.nnet)
# labels.nnet
# c s v
#c 22 0 3
#s 0 25 0
#v 3 0 22
# accuracy
mean(ird$species[-samp] == labels.nnet)
# 0.96
업데이트: 2016/4/28
Google의 TensorFlow는 신경망을 시각화 할 수 있는 매우 훌륭한 웹사이트를 공개했습니다 (여기를 참고).
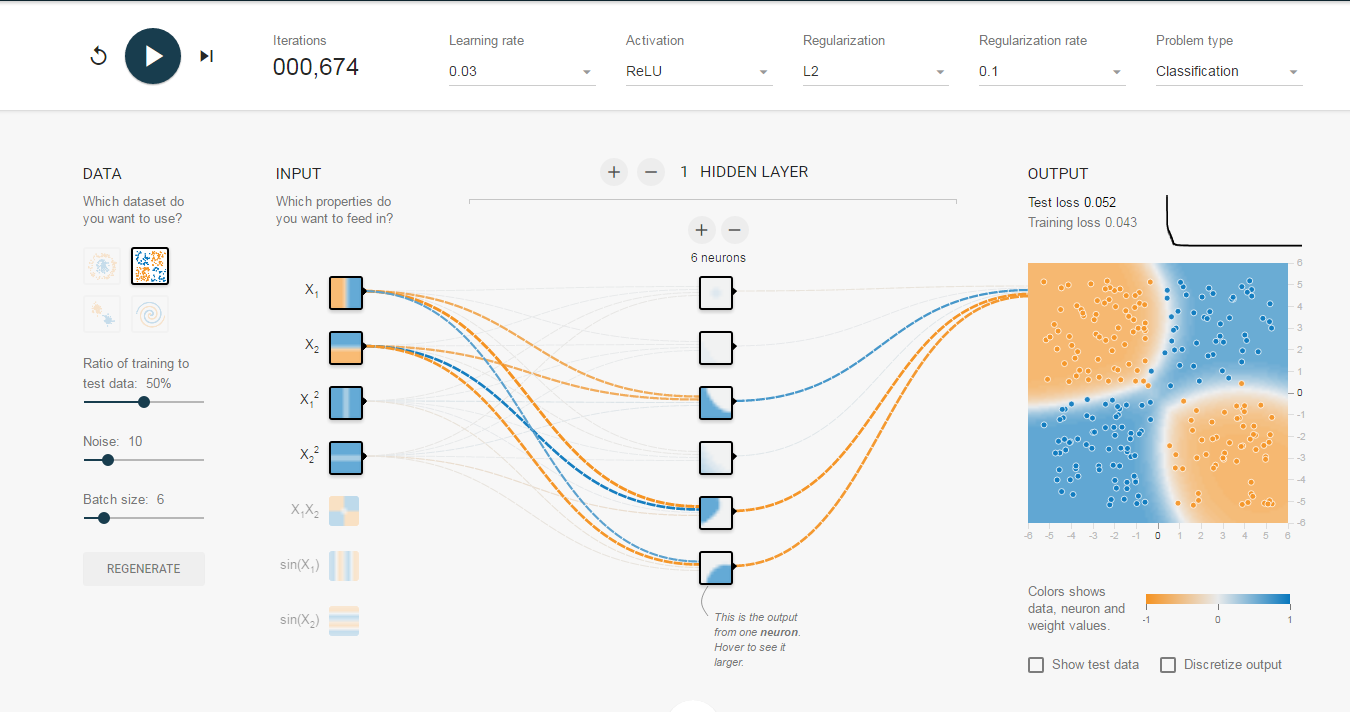
요약
이 글에서, 바닥에서부터 R의 신경망을 구현하는 방법에 대하여 알아보았습니다. 그러나 예제 코드는 단지 DNN의 핵심 개념을 구현한 것이며, 독자들은 다음과 같이 보다 심화된 연습을 할 수 있습니다:
- 다른 Classification 문제를 해결해 본다. 가령 여기의 테스트 케이스를 활용할 수 있습니다.
- 은닉 레이어 사이즈, 활성함수, 손실함수를 다양하게 선택해 봅니다.
- 단일 은닉 레이어 네트워크에서 다중 은닉 레이어로 확장해 봅니다.
- 회귀 문제를 해결하는 네트워크를 설계해 봅니다.
- 네트워크 아키텍쳐, Weights, Bias를 시각화 해봅니다. 여기를 참고하도록 합니다.
Source Codes
train.dnn.R
# Train: build and train a 2-layers neural network
train.dnn <- function(x, y, traindata=data, testdata=NULL,
model = NULL,
# set hidden layers and neurons
# currently, only support 1 hidden layer
hidden=c(6),
# max iteration steps
maxit=2000,
# delta loss
abstol=1e-2,
# learning rate
lr = 1e-2,
# regularization rate
reg = 1e-3,
# show results every 'display' step
display = 100,
random.seed = 1)
{
# to make the case reproducible.
set.seed(random.seed)
# total number of training set
N <- nrow(traindata)
# extract the data and label
# don't need atribute
X <- unname(data.matrix(traindata[,x]))
# correct categories represented by integer
Y <- traindata[,y]
if(is.factor(Y)) { Y <- as.integer(Y) }
# create index for both row and col
# create index for both row and col
Y.len <- length(unique(Y))
Y.set <- sort(unique(Y))
Y.index <- cbind(1:N, match(Y, Y.set))
# create model or get model from parameter
if(is.null(model)) {
# number of input features
D <- ncol(X)
# number of categories for classification
K <- length(unique(Y))
H <- hidden
# create and init weights and bias
W1 <- 0.01*matrix(rnorm(D*H), nrow=D, ncol=H)
b1 <- matrix(0, nrow=1, ncol=H)
W2 <- 0.01*matrix(rnorm(H*K), nrow=H, ncol=K)
b2 <- matrix(0, nrow=1, ncol=K)
} else {
D <- model$D
K <- model$K
H <- model$H
W1 <- model$W1
b1 <- model$b1
W2 <- model$W2
b2 <- model$b2
}
# use all train data to update weights since it's a small dataset
batchsize <- N
# init loss to a very big value
loss <- 100000
# Training the network
i <- 0
while(i < maxit && loss > abstol ) {
# iteration index
i <- i +1
# forward ....
# 1 indicate row, 2 indicate col
hidden.layer <- sweep(X %*% W1 ,2, b1, '+')
# neurons : ReLU
hidden.layer <- pmax(hidden.layer, 0)
score <- sweep(hidden.layer %*% W2, 2, b2, '+')
# softmax
score.exp <- exp(score)
# debug
probs <- score.exp/rowSums(score.exp)
# compute the loss
corect.logprobs <- -log(probs[Y.index])
data.loss <- sum(corect.logprobs)/batchsize
reg.loss <- 0.5*reg* (sum(W1*W1) + sum(W2*W2))
loss <- data.loss + reg.loss
# display results and update model
#if( i %% display == 0) {
if( 1 == 1 ) {
if(!is.null(testdata)) {
model <- list( D = D,
H = H,
K = K,
# weights and bias
W1 = W1,
b1 = b1,
W2 = W2,
b2 = b2)
labs <- predict.dnn(model, testdata[,-y])
accuracy <- mean(as.integer(testdata[,y]) == Y.set[labs])
cat(i, loss, accuracy, "\n")
} else {
cat(i, loss, "\n")
}
}
# backward ....
dscores <- probs
dscores[Y.index] <- dscores[Y.index] - 1
dscores <- dscores / batchsize
dW2 <- t(hidden.layer) %*% dscores
db2 <- colSums(dscores)
dhidden <- dscores %*% t(W2)
dhidden[hidden.layer <= 0] <- 0
dW1 <- t(X) %*% dhidden
db1 <- colSums(dhidden)
# update ....
dW2 <- dW2 + reg*W2
dW1 <- dW1 + reg*W1
W1 <- W1 - lr * dW1
b1 <- b1 - lr * db1
W2 <- W2 - lr * dW2
b2 <- b2 - lr * db2
}
# final results
# creat list to store learned parameters
# you can add more parameters for debug and visualization
# such as residuals, fitted.values ...
model <- list( D = D,
H = H,
K = K,
# weights and bias
W1= W1,
b1= b1,
W2= W2,
b2= b2)
return(model)
}
predict.dnn.R
# Prediction
predict.dnn <- function(model, data = X.test) {
# new data, transfer to matrix
new.data <- data.matrix(data)
# Feed Forwad
hidden.layer <- sweep(new.data %*% model$W1 ,2, model$b1, '+')
# neurons : Rectified Linear
hidden.layer <- pmax(hidden.layer, 0)
score <- sweep(hidden.layer %*% model$W2, 2, model$b2, '+')
# Loss Function: softmax
score.exp <- exp(score)
probs <-sweep(score.exp, 1, rowSums(score.exp), '/')
# select max possiblity
labels.predicted <- max.col(probs)
return(labels.predicted)
}
main.R
# Copyright 2016: www.ParallelR.com
# Parallel Blog : R For Deep Learning (I): Build Fully Connected Neural Network From Scratch
# Classification by 2-layers DNN and tested by iris dataset
# Author: Peng Zhao, patric.zhao@gmail.com
base::rm(list = ls())
base::gc()
source('./train.dnn.R', echo=FALSE)
source('./predict.dnn.R', echo=FALSE)
########################################################################
# testing
#######################################################################
set.seed(1)
# 0. EDA
summary(iris)
names(iris)
plot(iris)
# 1. split data into test/train
samp <- c(sample(1:50,25), sample(51:100,25), sample(101:150,25))
length(samp)
# 2. train model
ir.model <- train.dnn(x=1:4, y=5, traindata=iris[samp,], testdata=iris[-samp,], hidden=10, maxit=2000, display=50)
# ir.model <- train.dnn(x=1:4, y=5, traindata=iris[samp,], hidden=6, maxit=2000, display=50)
# 3. prediction
# NOTE: if the predict is factor, we need to transfer the number into class manually.
# To make the code clear, I don't write this change into predict.dnn function.
labels.dnn <- predict.dnn(ir.model, iris[-samp, -5])
# 4. verify the results
table(iris[-samp,5], labels.dnn)
# labels.dnn
# 1 2 3
#setosa 25 0 0
#versicolor 0 24 1
#virginica 0 0 25
#accuracy
mean(as.integer(iris[-samp, 5]) == labels.dnn)
# 0.98
# 5. compare with nnet
library(nnet)
ird <- data.frame(rbind(iris3[,,1], iris3[,,2], iris3[,,3]),
species = factor(c(rep("s",50), rep("c", 50), rep("v", 50))))
ir.nn2 <- nnet(species ~ ., data = ird, subset = samp, size = 6, rang = 0.1,
decay = 1e-2, maxit = 2000)
labels.nnet <- predict(ir.nn2, ird[-samp,], type="class")
table(ird$species[-samp], labels.nnet)
# labels.nnet
# c s v
#c 22 0 3
#s 0 25 0
#v 3 0 22
# accuracy
mean(ird$species[-samp] == labels.nnet)
# 0.96
# Visualization
# the output from screen, copy and paste here.
data1 <- ("i loss accuracy
50 1.098421 0.3333333
100 1.098021 0.3333333
150 1.096843 0.3333333
200 1.093393 0.3333333
250 1.084069 0.3333333
300 1.063278 0.3333333
350 1.027273 0.3333333
400 0.9707605 0.64
450 0.8996356 0.6666667
500 0.8335469 0.6666667
550 0.7662386 0.6666667
600 0.6914156 0.6666667
650 0.6195753 0.68
700 0.5620381 0.68
750 0.5184008 0.7333333
800 0.4844815 0.84
850 0.4568258 0.8933333
900 0.4331083 0.92
950 0.4118948 0.9333333
1000 0.392368 0.96
1050 0.3740457 0.96
1100 0.3566594 0.96
1150 0.3400993 0.9866667
1200 0.3243276 0.9866667
1250 0.3093422 0.9866667
1300 0.2951787 0.9866667
1350 0.2818472 0.9866667
1400 0.2693641 0.9866667
1450 0.2577245 0.9866667
1500 0.2469068 0.9866667
1550 0.2368819 0.9866667
1600 0.2276124 0.9866667
1650 0.2190535 0.9866667
1700 0.2111565 0.9866667
1750 0.2038719 0.9866667
1800 0.1971507 0.9866667
1850 0.1909452 0.9866667
1900 0.1852105 0.9866667
1950 0.1799045 0.9866667
2000 0.1749881 0.9866667 ")
data.v <- read.table(text=data1, header=T)
par(mar=c(5.1, 4.1, 4.1, 4.1))
plot(x=data.v$i, y=data.v$loss, type="o", col="blue", pch=16,
main="IRIS loss and accuracy by 2-layers DNN",
ylim=c(0, 1.2),
xlab="",
ylab="",
axe =F)
lines(x=data.v$i, y=data.v$accuracy, type="o", col="red", pch=1)
box()
axis(1, at=seq(0,2000,by=200))
axis(4, at=seq(0,1.0,by=0.1))
axis(2, at=seq(0,1.2,by=0.1))
mtext("training step", 1, line=3)
mtext("loss of training set", 2, line=2.5)
mtext("accuracy of testing set", 4, line=2)
legend("bottomleft",
legend = c("loss", "accuracy"),
pch = c(16,1),
col = c("blue","red"),
lwd=c(1,1)
)